Seguindo a nossa série “Dados O Novo Petróleo! Como extrair Valor?” Hoje vamos falar sobre Aprendizagem Não Supervisionada.
Atualmente são poucas as áreas de negócio onde a Inteligência Artificial não tenha tocado. A utilização da massa de dados das empresas, que tem crescido exponencialmente com os avanços tecnológicos, auxiliado as aplicações de algoritmos baseados em estatística, tem resolvido tarefas complexas demais para serem solucionadas por nós humanos.
Para resolver problemas com essa complexidade, o primeiro passo é coletar e tratar os dados que serão utilizados para treinamento desse algoritmo. Quanto maior a quantidade de dados apresentados e quanto maior a causalidade deles para ocorrência do problema em questão, melhor será o seu algoritmo final. Com os dados prontos, realiza-se uma separação da sua base, em treinamento e validação. A validação é isolada do ambiente em um primeiro momento e o treinamento é utilizado na capacitação do algoritmo para solver o problema. Quando o resultado do treinamento é satisfatório, seu algoritmo deverá ter adquirido a habilidade de generalizar as características do problema (se treinado corretamente), então lhes é apresentado a partição de validação e pode-se medir a sua capacidade, utilizando diversas métricas distintas (ex: Recall, Acurácia, Precisão, Curva ROC, etc.).
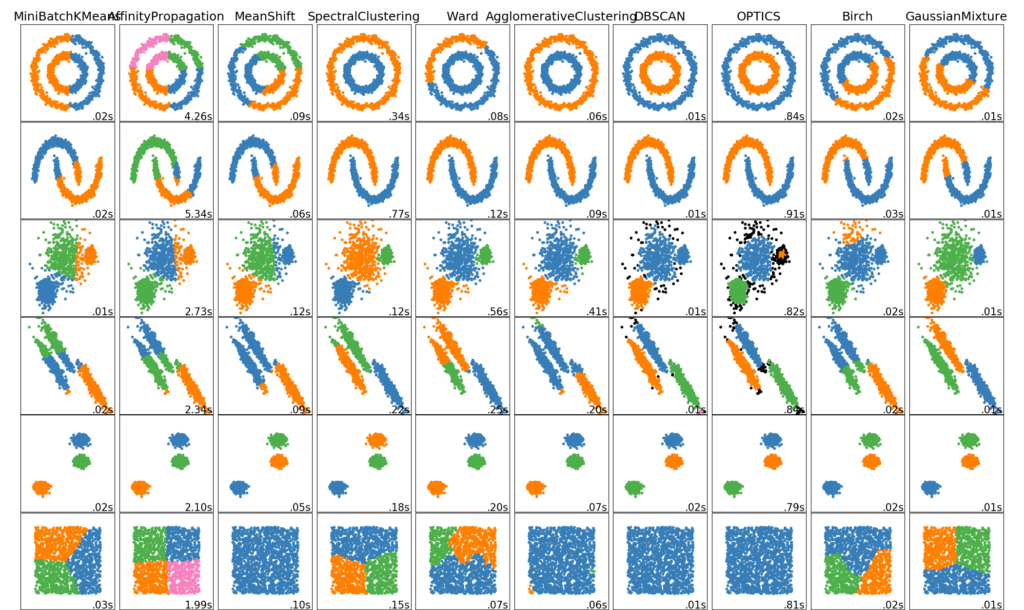
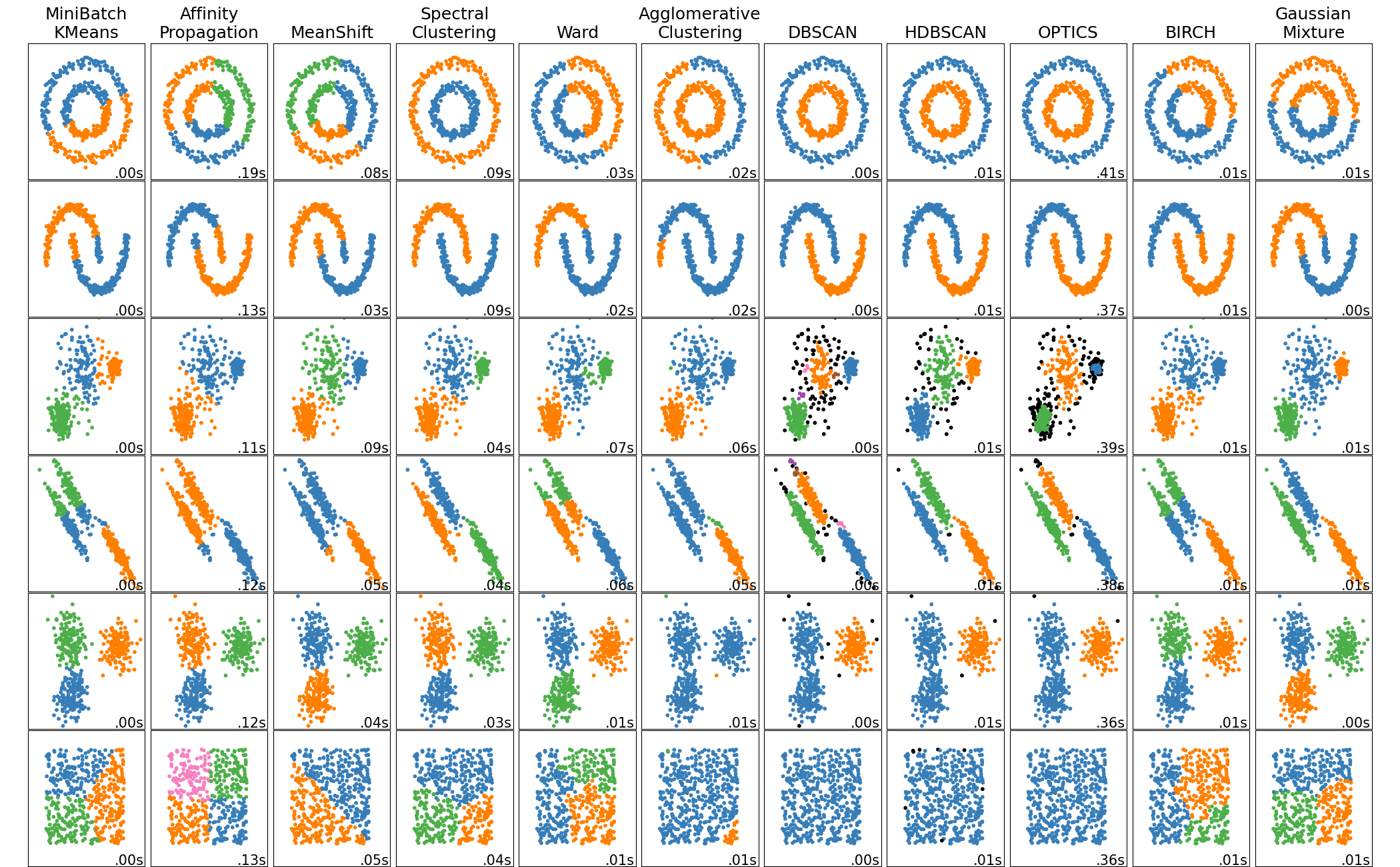
Mas quando não sabemos previamente quais valores nossa predição deve assumir? Quando queremos entender nossos dados e a partir deles, deduzir os modelos que possuímos para aquele problema? Nesse caso, o algoritmo deve encontrar estruturas e padrões, e então classificar os novos resultados a partir da similaridade das suas características, com os grupos descobertos no treinamento. Esse paradigma de aprendizado é conhecido como Aprendizagem Não-Supervisionada e é utilizada em diversos contextos como classificações e agrupamentos, recomendações, detecção de anomalias, redução de dimensionalidade e detecção de padrões e/ou regras associativas. Alguns exemplos de algoritmos são K-Means, Mean Shift, DBSCAN, PCA, UMAP etc. cada qual com as suas finalidades e particularidades. Abaixo temos uma imagem clássica de comportamentos de alguns algoritmos para classificação de grupos em alguns cenários:
Aplicação
Sobre algumas aplicações reais temos a Amazon, por exemplo, que aplica clustering dos seus clientes para realizar recomendações de vendas customizadas para cada um deles. Essa prática é muito comum e é utilizada também pela Netflix, Youtube e outras diversas empresas que recomendam produtos baseados nas experiências do usuário. Outro uso é a redução de dimensionalidade, onde o algoritmo “simplifica” os dados, reduzindo a dimensão do conjunto, tentando condensar a informação contida nas colunas e manter variação original dos dados intacta o máximo possível. Isso reduz, por exemplo, um conjunto de dados de 7 dimensões, para um conjunto de 3 dimensões, que pode ser visualizado e analisado graficamente. Por fim, mas não menos importante, temos a detecção de anomalias, que entende e agrupa uma série de comportamentos esperados e tenta detectar ações que fogem do padrão. Fraudes de cartão de crédito, detecção de doenças, defeitos em equipamentos, dentre outros problemas recorrem a essa estratégia.
Hands-on
É interessante pensar que todos os problemas de classificação com Aprendizagem Supervisionada, onde possuímos um conjunto discreto de categorias previamente determinadas e temos de classificar novas entradas, podem prontamente assumir um contexto de Aprendizagem Não-Supervisionada. Basta desconsiderarmos a coluna que pretendemos predizer, e deixar os dados nos guiarem aos grupos aos quais eles pertencem. Um conjunto de dados didático muito comum aos iniciantes em Data Science é o Iris Flower. Mesmo sendo um dataset extremamente controlado, ele compõe um ótimo cenário para exemplificarmos os conceitos exibidos anteriormente.
O problema no qual iremos resolver é classificar as Flores de Íris em três categorias: Versicolor, Setosa e Virginica, a partir do comprimento de largura das suas pétalas e sépalas.

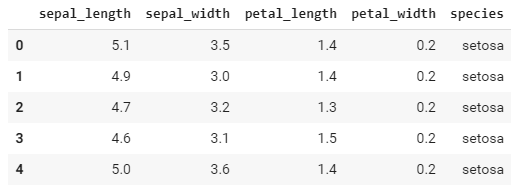
Então, basicamente temos um dataset composto por diversas observações de flores e a classificação de suas espécies (abaixo os primeiros 5 resultados do dataset):
Trata-se de um ambiente supervisionado, pois já possuímos a classificação das espécies que desejamos predizer, porém nada nos impede de transformá-lo em um ambiente não-supervisionado e analisarmos o comportamento dos nossos algoritmos. Mas antes de realizar essa alteração, vamos visualizar as correlações que possuímos:
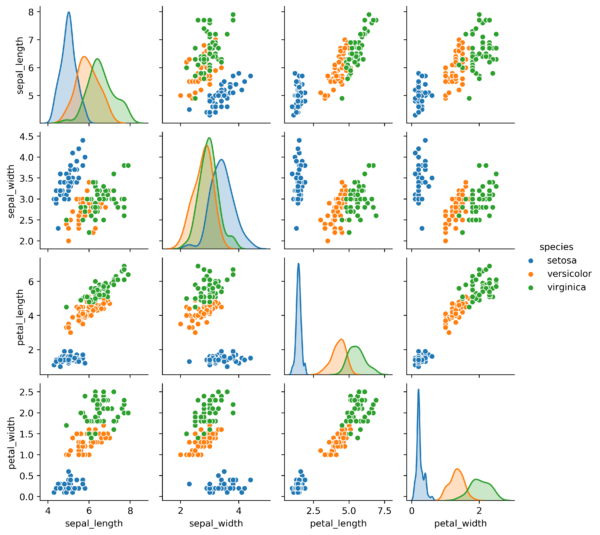
Observando primeiramente a diagonal principal, podemos perceber que existe uma boa separação nas variáveis da classificação indicada, ou seja, existe pouca sobreposição gráfica entre as entradas de classes distintas, o que facilita visualizar os efeitos isolados das variáveis independentes na variável dependente. Analisando em seguida os gráficos de dispersão, concluímos que existe pouca intersecção entre as entradas de classes distintas, viabilizando uma boa classificação.
Supondo que você deseja apresentar esse dataset e sua distribuição para um supervisor que não conhece muito sobre o assunto. Você precisa apresentar um gráfico para que ele entenda a classificação das flores e comportamento que ela assume em cada uma delas. Você possui um problema de 4 dimensões (comprimento da pétala, largura da pétala, comprimento da sépala e largura da sépala), e não é trivial representar graficamente essa quantidade de dimensões. Uma solução? Utilizar uma redução de dimensionalidade para trazer esse contexto de maneira mais fiel possível para uma quantidade de dimensões viáveis de serem representadas e compreendidas graficamente. Aplicando um PCA (Principal Component Analysis), por exemplo, podemos reduzir a dimensionalidade de 4 para 2 dimensões, como observamos na imagem abaixo.
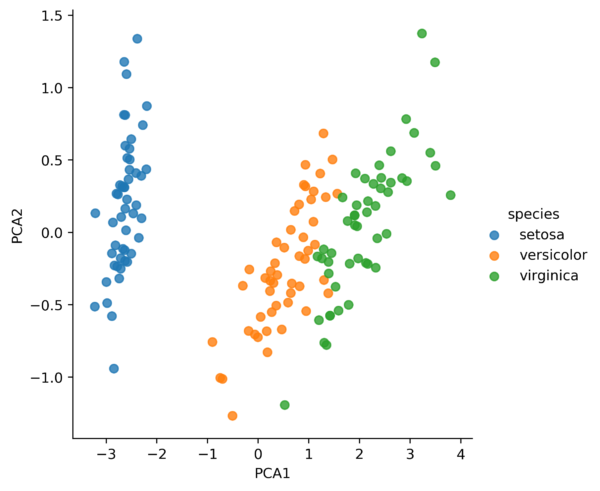
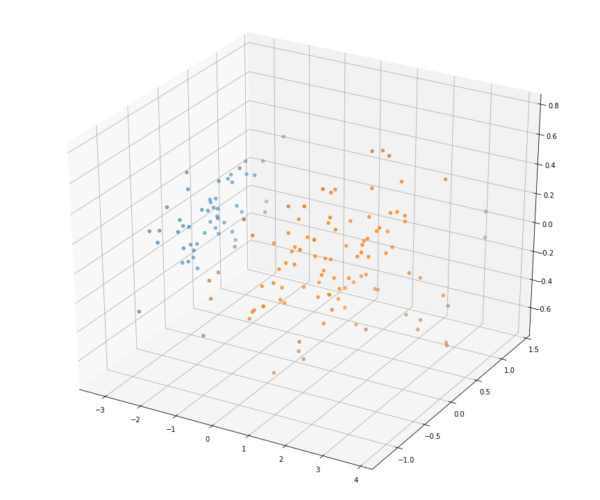
Estamos representando agora todos as entradas do dataset em duas novas dimensões PCA1 e PC2 que condensam as informações das 4 antigas. Vamos alterar as dimensões para 3 e analisar em um gráfico 3D, como seria o resultado do PCA nesse caso:
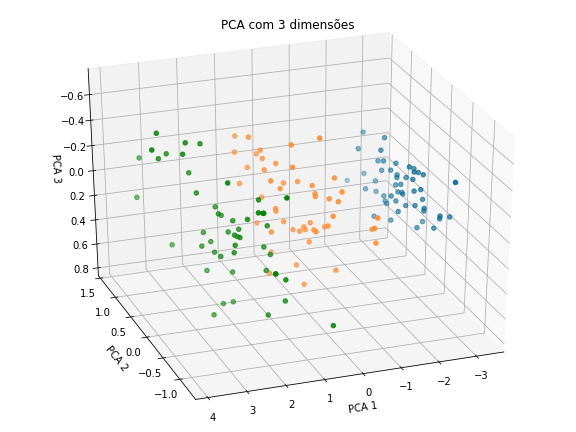
Agora temos uma nova representação das flores de íris em PCA1, PCA2, PCA3. Com nosso dataset reduzido, já podemos materializar nosso problema com gráficos, então partimos agora para o treinamento do nosso modelo. Como eliminamos a variável dependente para transformar nosso ambiente em um cenário não supervisionado, vamos utilizar o algoritmo simples K-Means, que consiste na inicialização randômica de um número k de centróides, que são os grupos que queremos classificar os dados. Depois, calcula-se a distância de todos os pontos para cada centróide e determinamos a quais clusters eles pertencem, baseado na menor distância aos centróides. Por fim, os centróides tem suas posições atualizadas para a média de todos os pontos pertencentes ao cluster e esse processo é repetido até que se estabilize, ou seja, nenhum centróide se movimente mais. Aplicando essa técnica, chegamos ao seguinte resultado:
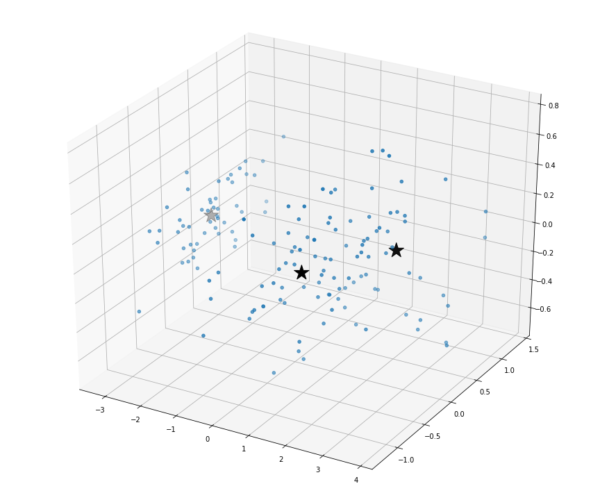
Os pontos marcados com estrelas, são os 3 centróides que determinamos para o problema. Eles assumiram as posições indicadas no gráfico. Será que ele conseguiu generalizar as informações do nosso dataset corretamente? Vamos analisar o mesmo gráfico, agora aplicando a classificação de variável dependente que removemos anteriormente:
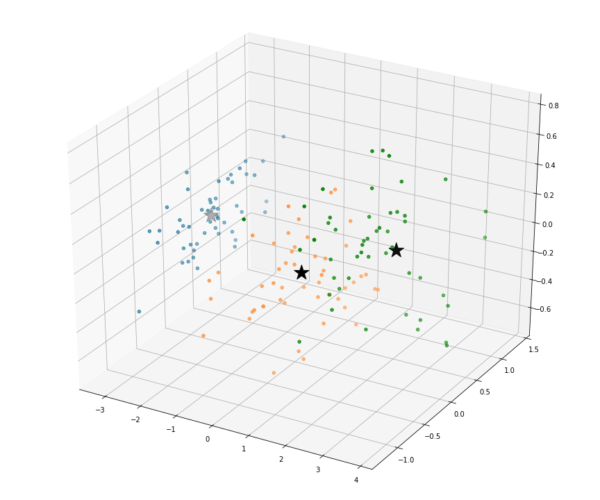
Conseguimos então visualizar que os centróides descobertos pela similaridade dos dados fazem sentido e se dispõe ao centro das classificações reais da Flor de Íris. Utilizamos um dos métodos mais simples de clusterização para classificar um dataset supervisionado e conseguimos validar que ele realmente trouxe um resultado válido para solução do problema. Vamos então agora utilizar um outro algoritmo, chamado HDBSCAN, que é considerado mais complexo e apresenta resultados melhores em diferentes cenários com relação ao K-Means. Ele se baseia na densidade dos pontos próximos para estipular os cluster e não precisamos passar o número de centróides previamente. Iremos utilizá-lo em seu modo padrão, sem alterarmos nenhum hiperparâmetro. Obtemos o seguinte resultado:
Percebemos que ele não conseguiu capturar a diferença entre os dois clusters: Versicolor (laranja) e Virginica (verde), como esperávamos para esse problema. Porque o algoritmo que é mais complexo, tem mais capacidade e apresentou melhores resultados não conseguiu convergir nessa classificação tão simples? Realizamos o mesmo treinamento nos dois algoritmos, com os mesmos dados, onde erramos? Como entendemos o seu funcionamento, conseguimos então deduzir onde ele pode ter falhado. Como existe uma intersecção entre Versicolor e Virginica, ele não conseguiu identificar uma quebra de densidade entre as duas massas de dados. A configuração dos hiperparâmetros é essencial para o funcionamento do algoritmo, talvez com um menor raio para identificação de densidade, seria possível solucionar corretamente. Entender suas características e realizar os ajustes finos para que ele se molde ao problema é de extrema importância.
O exemplo apresentado nos mostra que não basta apenas aplicar os melhores algoritmos para resolver problemas, a Ciência de Dados é um ramo onde devemos estudar tanto nossos problemas, quanto nossos algoritmos para entendermos e interpretarmos o funcionamento e resultado de cada caso. Se todos os problemas fossem resolvidos apenas aplicando os melhores algoritmos, não existiria a necessidade dos cientistas de dados. Ter conhecimento das possibilidades, saber modelar problemas e conhecer os algoritmos são o grande desafio da área e a combinação dessas habilidades formam os profissionais que conquistarão os melhores resultados.
Bibliografia
https://pythonistaplanet.com/applications-of-unsupervised-learning/
https://medium.com/@srishtisawla/iris-flower-classification-fb6189de3fff
Guilherme Costi
